☰

languageshare printsearch

Belastingen in silo's

Belastingen op silowanden; EN 1991-4; Belastingen op inbouwelementen in silo’s en storthopen

Dit document behandelt belastingen in silo's. Naast een beschrijving van de geldende normen worden enkele speciale belastingssituaties besproken, zoals bijvoorbeeld inbouwelementen.
Zie ook bulktechnologie met: definitie van stortgoed, ofwel bulk solids, eigenschappen, meetmethoden, silo-ontwerp.
En fenomenen in silo's bij opslag van bulkgoed over problemen, oplossingsrichtingen en enkele praktijkcases, o.a. over silodrukverlaging.

Belastingen op silowanden, de basis

Stromingsgedrag van bulkgoed zorgt voor onzekere drukken

Introductie

Bij de bouw van de eerste grote silo’s voor de opslag van graan in het midden van de 19e eeuw, gingen ze er nog vanuit dat bulkgoederen zich als vloeistoffen gedragen. Ze hielden dus rekening met een hydrostatisch drukverloop. Dat bleek een misverstand, er bleek ook sprake van de schuifspanning aan de wand. In 1895 ontwikkelde de Duitse ingenieur Janssen een theorie die nog steeds de basis is voor huidige berekeningen.

De klassieke Janssen-theorie

Omstreeks 1895 verrichtte Janssen een aantal metingen bij vierkante houten graansilo’s waarbij met verschillende vulhoogtes de druk op de vlakke bodem met een weegschaal werd bepaald. De gemeten bodemdrukken bleken hierbij minder dan lineair met de vulhoogte toe te nemen. Bij een voldoende hoge silo kwam de bodemdruk zelfs nooit boven een bepaalde maximale waarde uit.
In zijn theoretische analyse nam Janssen aan dat de verticale druk gelijkmatig verdeeld is over de omtrek en hij bekeek het verticale evenwicht over een schijf materiaal zoals aangegeven in afbeelding 1. Uit de evenwichtsvergelijking kunnen de klassieke formules voor de belastingen worden afgeleid. Hieruit blijkt dat de spanningen minder dan lineair met de diepte toenemen. Bij een grote diepte ten opzichte van de diameter bereiken de drukken een maximale waarde. Deze diepte en de daar optredende belastingen wordt bepaald door de verhouding van oppervlak en omtrek van de silo, de wrijving met de wand, de bulkdichtheid en de spanningsverhouding. De laatstgenoemde is de afhankelijkheid tussen horizontale druk en de verticale druk, een factor die constant wordt verondersteld. Deze factor wordt in silotheorieën meestal aangegeven met λ (lambda). In de Euronorm wordt deze K genoemd.
Het toepassen van deze formules vraagt correcte waarden van de wandwrijving, de spanningsverhouding en de bulkdichtheid om een redelijke benadering van de silodrukken te krijgen. Verder wordt in feite alleen naar de vulsituatie gekeken en geen rekening gehouden met het dynamische gedrag van het materiaal tijdens het leeglopen.

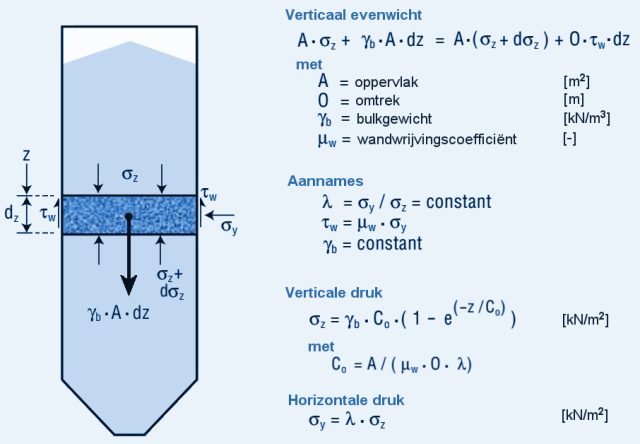
Modificaties van de silotheorie

Het Janssen-model voldeed tot ca 1950 redelijk maar daarna leidde de ontwikkeling van en betere kennis over constructiematerialen en methoden tot lagere veiligheidsfactoren. Hierdoor werd ook een betere bepaling van de belastingen noodzakelijk. Dit resulteerde in een veelvoud aan theoretisch en experimenteel onderzoek waaruit al ras bleek dat het probleem van silobelastingen erg complex was en er niet snel een exacte oplossing zou komen. De voorgestelde oplossingen waren steeds gebaseerd op vereenvoudigingen en soms simpele benaderingen. Ze hebben zeker bijgedragen tot een beter begrip van het probleem.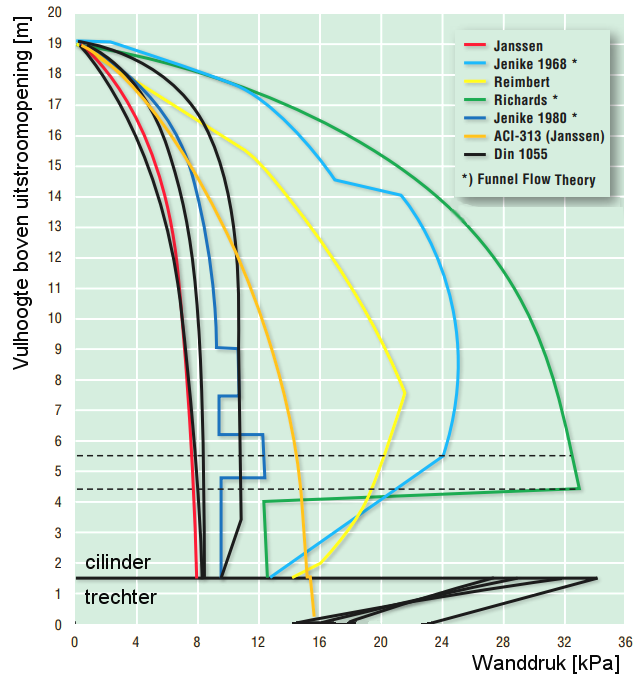

Duidelijk was dat er verschillen bestonden tussen de vul- en de leegloopsituatie, dat het stromingspatroon invloed had op de belastingen en dat wijzigingen in het interne spanningsverloop, bijvoorbeeld door een verandering van de doorsnede of inbouwelementen, gepaard konden gaan met hoge, lokale wandspanningen. Tevens werd onderkend dat door het dynamische gedrag tijdens het uitstromen, de spanningen ook grote variaties vertoonden. Deze nieuwe inzichten leiden in veel landen tot praktijkregels en normen die niet altijd eenvoudig toepasbaar bleken en bij vergelijking tot nogal verschillende resultaten leiden. Als voorbeeld is in de figuur hiernaast de wandbelasting weergegeven zoals in de jaren 80 berekend volgens een aantal toen bekende methoden of codes.

Het is duidelijk dat de keuze van de norm een bepalende factor in de berekende wandbelasting is.

Stroming en wandbelastingen

Zoals gezegd, gelden de klassieke Janssen-formules in feite alleen voor de vulsituatie. Tijdens het vullen van een silo zal het bulkmateriaal in verticale zin wat in elkaar worden gedrukt vanwege de druk van bovenliggende lagen. De grootste spanning zal in deze situatie daarom verticaal gericht zijn, we spreken dan van een actief spanningsveld. Wanneer nu de uitlaatklep wordt geopend of de losapparatuur gestart, en het bulkgoed in de trechter gaat stromen, ontstaat een andere situatie. Het stortgoed zal in verticale richting expanderen, en op de overgang van cilinder naar trechter wordt het horizontaal samengedrukt. De grootste spanning past zich bij de vervorming aan en zal nu horizontaal zijn, een zogenaamd passief spanningsveld. Deze omslag van actief naar passief zal onderin de trechter beginnen en doorzetten tot aan de overgang naar de cilinder. Een verdere omslag treedt in principe niet op omdat stortgoed in de cilinder niet hoeft te vervormen. Hier is dus een overgangsgebied. In dit gebied kan een forse, lokale piekspanning op de wand optreden, die onderin de trechter begint en bij de overgang als continue piek blijft werken, de zg. switch-belasting. Deze piekspanningen zijn ook theoretisch af te leiden uit de Janssen-vergelijkingen. Ze zijn in de praktijk experimenteel gemeten. Helaas is de exacte grootte van deze spanningspieken en het wandgedeelte waarover ze werkzaam zijn niet nauwkeurig vast te stellen.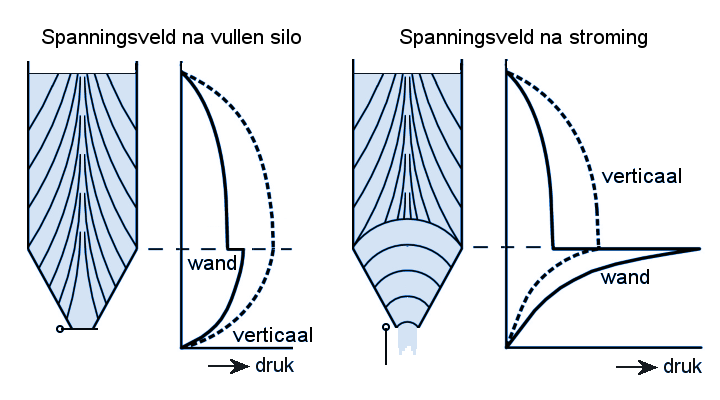

Deze lokale piekspanningen ter plaatse van de overgang cilinder/conus zijn meestal geen probleem voor de siloconstructie, omdat die daar door de geometrie al sterker is, en vaak ook wordt verstevigd, zeker wanneer de silo op poten wordt afgesteund. Bovenstaande geldt vooral wanneer de gehele massa in de silo in beweging is (massastroming) maar ook in het geval van kernstroming kunnen dergelijke piekspanningen wel voorkomen. Dan wordt er meestal een trechter in het bulkmateriaal zelf gevormd. Waar deze trechter de silowand raakt, zal het overgangsgebied van omslag van spanningsveld groter zijn, waardoor de piek kleiner is en/of over een groter gebied wordt uitgesmeerd. In gangbare normen wordt een piekbelasting bij kernstroming niet meegenomen in de cilinder, maar wordt vanwege ongelijkvormigheid van belastingen wel met een grotere factor gerekend. In de DIN 1055-6, lang de norm voor berekeningen, en nog steeds bruikbaar omdat het een bijlage van de EN 1991-4 is, wordt bij massastroming een pieklast meegenomen onderin de cilinder. In de berekening van de EN 1991-4 komt de piek niet hoger dan bovenin de trechter.

Silonormen

Meerdere landen stelden in de loop der tijd silonormen op om een eenduidig uitgangspunt te stellen om silobelastingen te berekenen. In Nederland bestonden wel plannen voor een eigen norm maar deze plannen zijn ingehaald door de Euronorm EN 1991-4. Lang is gebruik gemaakt van de DIN 1055, deel 6. Deze norm, voor het eerst uitgekomen in 1964 en gebaseerd op de theorie van Janssen, maakte wel onderscheid tussen de vul- en de leegstroomsituatie en hield rekening met de invloed van een excentrische uitloop. Nadeel was dat het toepassingsgebied zich beperkte zich tot vrijstromende en licht cohesieve materialen. In de praktijk komen echter veel cohesieve materialen voor, en bij een gebrek aan andere opties werd de DIN 1055-6 dus toch ook daarvoor toegepast. Een ander bezwaar van deze norm was dat de wandwrijvingshoek niet apart werd beschouwd maar als deel van de inwendige wrijvingshoek berekend.
In 1977 kwam vooruitlopend op een complete herziening van de norm, een serie aanvullende voorschriften uit. Hierin werd nogmaals aangegeven dat organisch cohesieve materialen niet volgens de norm mochten worden berekend. De vraag bleef hoe dan wel. Bovendien werd in de voorschriften een aantal toeslagfactoren ingevoerd. In 1987 verscheen een geheel nieuwe versie waarin een redelijk bruikbare berekenmethode werd gepresenteerd voor zowel de cilinder als de trechter. Deze versie voorzag een stromingspatroon met mogelijk optredende piekspanningen bij massastroming. Door een aantal toeslagen werd het dynamische gedrag tijdens uitstromen via een ongelijkvormige belasting verrekend.
De norm vermeldde voor twaalf materialen de benodigde gegevens terwijl in een aanvullend commentaar nog een (niet officiële) tabel werd gegeven met de relevante waarden voor twaalf andere materialen. Belangrijk nadeel vormt de berekening van de ongelijkmatige belasting met de factor die de ‘boosaardigheid’ van het materiaal weergeeft. Deze factor is niet te meten aan het materiaal maar moet met (full scale) tests of door vergelijking worden bepaald. Voor de in de tabel ontbrekende stortgoederen werd opgemerkt dat de gegevens hiervan via vergelijking met bekende producten of via meting moesten worden vastgesteld. Voor sterk cohesieve materialen mag de norm worden toegepast indien de zekerheid bestaat dat de uitstroming geen problemen zal opleveren. Voor dit type materialen werd aanbevolen de benodigde eigenschappen met een shear-cell te meten en op basis hiervan de silo te dimensioneren. Werken met de norm leek redelijk maar bleek in de praktijk toch nog wel eens mis te lopen met forse beschadigingen aan silo’s als gevolg.

Euronorm

Om in Europa eenheid te brengen in de veelheid van berekeningsmethoden en normen, startten eind jaren 80 de eerste gesprekken voor een Europese norm, binnen het geheel van de Eurocode. De Eurocode EN 1990 geeft grondslagen van het constructief ontwerp, en stelt de beginselen van eisen van veiligheid, bruikbaarheid en duurzaamheid van constructies vast, omschrijft de grondslagen voor hun ontwerp, berekening, en toetsing en geeft richtlijnen voor samenhangende aspecten van de constructieve betrouwbaarheid. EN 1990 is bedoeld om te worden gebruikt in samenhang met EN 1991 tm EN 1999. Met EN 1991 zijn uiteenlopende belastingen (bijv. wind en aardbeving) te bepalen, hier vallen de silobelastingen ook onder. Deze worden behandeld EN 1991-4 Belastingen op constructies; silo's en opslagtanks.

Belastingen in silo’s volgens de Euronorm

Bespreking van de EN 1991-4

Introductie

Sinds het begin van de jaren negentig is er in Europees verband gewerkt aan een serie normen over belastingen op constructies en bouwwerken om eenheid te brengen in de technische grondslagen en veiligheidseisen in de EU. Dit is de Euronorm, serie EN 1990 - EN 1999. Met EN 1991 zijn uiteenlopende belastingen (bijv. wind en aardbeving) te bepalen. Voor silobelastingen is de EN 1991-4 Belastingen op constructies; silo's en opslagtanks. In dit artikel wordt de berekening van silo’s besproken.

NEN EN 1991-4

Nadat in de negentiger jaren een aantal voorlopige versies van normen over belastingen op constructies en bouwwerken voor commentaar werd uitgegeven, is in mei 2006 een geheel vernieuwde versie gepubliceerd die de eerste definitieve Nederlandse norm voor berekening van silobelastingen is geworden, als NEN-EN 1991-4:2006. In september 2013 is de meest recente versie van de bijbehorende Nationale bijlage verschenen. Van Europese normen bestaan drie officiële versies: Engels, Frans en Duits. Voor Nederland zal de Engelse versie gelden. In maart 2024 is een Europees normontwerp gepubliceerd, de prEN 1991-4:2024,IDT, waarop voor 1 mei 2024 commentaar kon worden geleverd. Wanneer dit ontwerp definitief wordt gemaakt, zal deze ook als Nederlandse norm gelden. In de eerste paragraaf van deze versie is een opmerking toegevoegd: NOTE 1 Silos are used for the storage of particulate solids: tanks are used for the storage of liquids. Voor de bulktechnoloog (wellicht) een open deur, maar in de praktijk niet zo bekend.
Dit artikel beschrijft in hoofdlijnen de inhoud van de huidige norm voor silobelastingen, om de lezer enige achtergrond te bieden.

Toepassingsgebied en beperkingen

De norm zal moeten worden toegepast in samenhang met de overige Euronormen uit de serie EN 1991 tot EN 1999 waarin andere aspecten, zoals materiaalkeuze en algemene veiligheidseisen, aan de orde komen. De norm geeft algemene richtlijnen voor bepalen van belastingen voor het op sterkte en stijfheid ontwerpen van silo’s voor opslag van stortgoed (particulate solids) en van tanks voor de opslag van vloeistoffen. In dit verhaal laten we tanks verder buiten beschouwing en beperken we ons tot silo’s.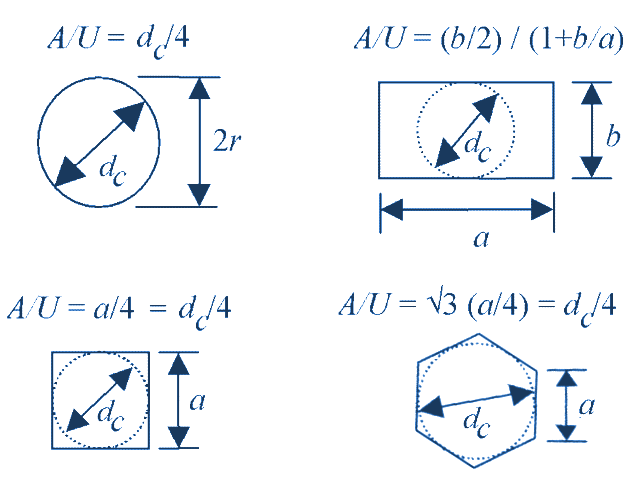

Toepassing van de norm is wat de geometrie betreft beperkt tot:

• Silo's waarvan de dwarsdoorsnede rond, vierkant, rechthoekig of zeskantig is. Kleine afwijkingen van deze vormen zijn toegestaan voor zover met de gevolgen voor de spanningen rekening wordt gehouden. Zie afbeelding 1.
• Silo's waarvoor geldt dat de hoogte niet meer dan tien maal de diameter (ofwel ingeschreven cirkel) is.
• de silodiameter moet onder de 60 m blijven, terwijl de totale hoogte niet groter moet zijn dan 100 meter.
• De overgang van cilinder naar trechter moet in één horizontaal vlak liggen.
• De silo’s mogen geen ingebouwde elementen, zoals een omgekeerde conus of piramide of interne dwarsbalken, hebben. Alleen in rechthoekige silo’s zijn wel spandraden / trekstangen toegestaan
• De trechter dient conisch, piramidevormig of wigvorming (wedge-shaped) te zijn. Bij andere vormen en bij ingebouwde elementen moet extra aandacht worden gegeven.

Verder wordt er nog een aantal eisen aan het stortgoed en het gebruik van de silo gesteld:

• Elke silo wordt ontworpen voor een afgebakende groep stortgoederen.
• Het stortgoed moeten vrijstromend zijn, of het ontwerp is zodanig dat vrije stroming kan worden gegarandeerd in de silo. Of het stortgoed moet er langs de bovenkant weer uitgehaald worden.
• De maximale deeltjesdiameter van het stortgoed mag niet groter zijn dan drie procent van de silodiameter
• Bij het vullen of legen van de silo mogen geen merkbare traagheids- of impactbelastingen optreden

Ten slotte wordt nog aangegeven dat invloeden van aardschokken, interne schokken of trillingen niet door de norm worden gedekt. De norm kan ook niet worden gebruikt om een silo qua stromingsgedrag te ontwerpen. Bovengenoemde beperkingen kwamen in eerdere normen ook voor en zijn dusdanig ruim dat de meeste silo’s wel onder de norm zullen vallen. Wel valt op te merken dat van lang niet alle in de praktijk gebruikte soorten stortgoed de eigenschappen bekend zijn. Ook is het lastig dat bijvoorbeeld interne schokken op voorhand niet te voorspellen zijn.

Classificatie en ontwerpsituaties

Bij de berekening van de belastingen op een silo zal volgens de norm moeten worden uitgegaan van de silovorm, de eigenschappen van het stortgoed en het optredende stromingspatroon. De druk vanuit het stortgoed wordt in de norm opgebouwd uit een symmetrisch en een a-symmetrisch deel (patch load). Bij grote excentriciteiten wordt de totale belasting als niet symmetrisch beschouwd. In de norm wordt verder een indeling naar veiligheidsklassen (Action Assessment Classes)aangegeven, gebaseerd op grootte en excentriciteit. Silo’s met een opslagcapaciteit groter dan 10.000 ton, of met grote excentriciteiten vallen onder klasse 3. Silo’s met opslagcapaciteit kleiner dan 100 ton vallen in klasse 1. De overige silo’s zijn klasse 2. Deze classificatie hangt samen met de algemene veiligheideisen voor constructies zoals neergelegd in de normen EN 1992 en EN 1993.

De belastingen door bulkgoed op een silo bestaan uit normaaldrukken en schuifkrachten op de cilinderwand, trechterdrukken en een maximale bodembelasting. Parameters in de berekening zijn: de wandwrijving op de betreffende wand, de soortelijke massa (bulkdichtheid, stortgewicht), de inwendige wrijving, en de spanningsfactor K (verhouding tussen horizontale en verticale drukken) van het stortgoed.
Elk van deze grootheden kent in principe een onder- en bovengrens. Voor elke belastingsituatie geeft de norm aan van welke combinatie van grenswaarden moet worden uitgegaan om tot de hoogste belasting te komen. Voor silo’s in veiligheidsklasse 1 (dus kleiner dan 100 ton) mag echter voor de genoemde parameters van een gemiddelde waarde worden uitgegaan, behalve voor de dichtheid .

Verder wordt rekening gehouden met het type stroming dat optreedt in de silo. Onderscheid wordt gemaakt in massastroming (mass flow, plug flow), pijpstroming (kernstroming, core/funnel flow) en gemengde stroming. Bij gemengde en de pijpstroming wordt een verdere indeling naar de mate van excentriciteit gemaakt.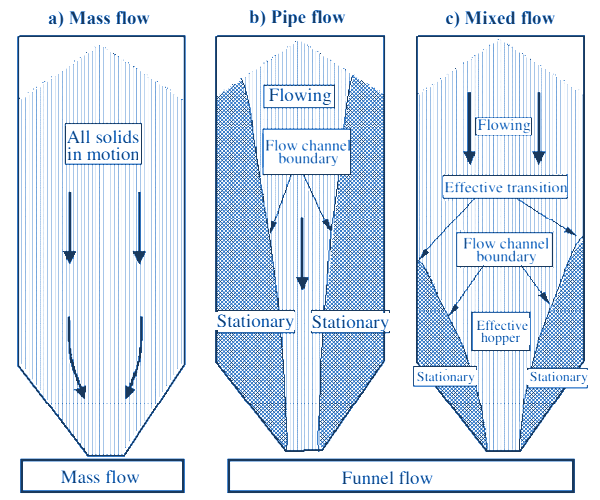

Een verdere indeling is die naar de vorm van de silo, zie afbeelding 3. Onderscheiden worden hier horizontale silo’s, waarbij de wanden als keerwand fungeren, vlakke silo’s en slanke tot zeer slanke silo’s, de laatste met de mogelijkheid van kanaalvorming (ratholing) door asymmetrische vulling. Als laatste wordt nog gekeken naar bijzonderheden als pneumatisch vullen, luchtinjectie of interne mechanische uitdraagsystemen. Voor al deze categorieën wordt in de norm aangegeven op welke wijze de belastingen moeten worden berekend.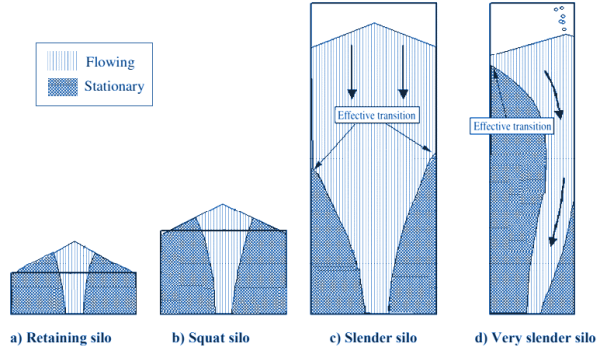

Toepassing van de stortgoedeigenschappen

Een verschil met eerdere normen is de nadruk op de eigenschappen van het stortgoed, en met name over het meten ervan. De norm noemt twee mogelijkheden. De makkelijkste manier is gebruik te maken van de in Annex E gegeven tabel, waarin voor 24 soorten stortgoed de benodigde waarden en eventuele toeslagfactoren zijn vermeld. In deze tabel staan tevens de gegevens voor een zogenaamd standaardmateriaal, die kunnen worden gebruikt indien de kosten voor het testen van de werkelijke producten niet goed zijn te rechtvaardigen. Gebruik van dit “default material” wordt alleen aangeraden bij kleine silo’s, omdat bij grotere silo’s wel erg oneconomische ontwerpen ontstaan. Er wordt bijvoorbeeld gerekend met een stortgewicht van 2200 kg per kubieke meter, hetgeen drie à vier maal zo zwaar is als de meeste soorten veevoer of plastics.
De andere manier is het op een voorgeschreven wijze meten (of laten meten) van het opgeslagen stortgoed. In Annex C worden methoden genoemd waarmee verschillende eigenschappen gemeten kunnen worden Deze moeten worden gevolgd voor silo's in Action Assessment Class 3 en als het stortgoed niet in tabel E.1 staat en het default material een te dure constructie zal opleveren. Waarden uit metingen mogen altijd als alternatief voor de vereenvoudigde waarden in tabel E.1 worden gebruikt. Een representatief monster is van belang. Er wordt onderscheid gemaakt in waarden voor bepaling van belastingen en voor bepaling van het stromingpatroon.

Het meten van de wandwrijving

De norm onderscheidt vier typische wandmaterialen:

1. Gladde wanden (slippery), zoals rvs, coatings, HDPE of gepolijst aluminium;
2. Middelgladde wanden (smooth), zoals glad constructiestaal, geoxideerd aluminium;
3. Ruwe wanden (raspy), zoals beton, geroest staal, keramische tegels;
4. Onregelmatige wanden, zoals gegolfde platen of damwanden.

De te volgen testmethode wordt beschreven in Annex C van de norm en komt overeen met een standaard shear-test. De nadruk wordt gelegd op het meten bij de juiste drukken en aan de juiste wandmaterialen. In geval van bijvoorbeeld een damwand kan de wandwrijving als een gewogen gemiddelde van gemeten wandwrijving en inwendige wrijving worden berekend.

Het meten van de inwendige wrijving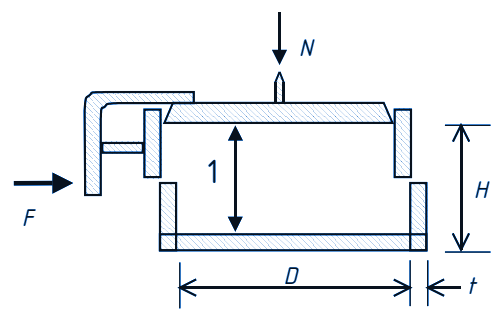

Voor het meten van de inwendige wrijving wordt in eerste instantie een “direct shear test” genoemd. De toe te passen normaaldruk en de te volgen testmethode wordt aangegeven, om de inwendige wrijving en de cohesie te bepalen. Een triaxiaal test mag ook gebruikt worden. Als alternatief wordt een “indirecte meting” met de Jenike shear cell (met gestandaardiseerde meetprocedure volgens ASTM D 6128) gegeven. Deze Jenike shear cell is exact de tester zoals aangegeven bij de direct shear test. Het verschil tussen de directe en indirecte test lijkt daarmee de gebruikte procedure.

Het meten van de bulkdichtheid

De bulkdichtheid kan worden gemeten door het materiaal in een niet te hoge cilinder (diameter circa tweemaal de hoogte) via een bovendeksel te belasten en het volume te meten. Ook hier worden methode en toe te passen drukken aangegeven. De Jenike shear cell voldoet hieraan, en het verloop van de bulkdichtheid wordt bekend als hiermee de brugvormingsgedrag wordt gemeten.

Het meten van de spanningsfactor K

De factor K geeft de verhouding tussen de horizontale en verticale spanning in een silo. Deze factor kan in principe worden gemeten met een apparaat zoals aangegeven in de norm. In dit apparaat wordt een stortgoedmonster verticaal belast met een spanning σ1 en wordt de horizontale spanning gemeten. Dit laatste gebeurt door de rek in de dunwandige cilinder te meten met rekstrookjes. Het is duidelijk dat deze methode voor het meten van K nu niet direct simpel is. Sterker nog, vanuit onderzoek aan de Universiteit Twente is bekend dat een tester die dit kan meten, erg moeilijk te maken is en de meting zelf tijdrovend en slecht reproduceerbaar is. Resultaat is namelijk een wolk van meetpunten, zodat deze factor net zo goed op een andere manier kan worden geschat. Gelukkig wordt dit in de norm ook onderkend. Een benaderde waarde van K kan als alternatief uit de inwendige wrijving worden berekend.

Berekening van de belastingen

Eenmaal in het bezit van de juiste gegevens van het stortgoed, kunnen op basis van de silovorm, de grootte, het stromingspatroon en mogelijke speciale voorzieningen alle relevante silobelastingen worden berekend. In de norm staan nagenoeg voor alle gevallen de te volgen berekeningsmethoden nauwkeurig omschreven. In een aantal gevallen zijn ook toelaatbare alternatieven gegeven. Voor producten waarbij mogelijk stofexplosies op kunnen treden, volgt ten slotte nog een aantal adviezen voor een zo veilig mogelijk ontwerp.

Conclusie

We concluderen dat deze norm voor bijna alle voorkomende gevallen een adequate berekeningsmethode geeft voor het bepalen van de silobelastingen. Er zitten echter nog wel wat addertjes onder het gras. In de eerste plaats is het gebruik van de norm niet bepaald eenvoudig. Mede door de nagestreefde compleetheid (de norm beslaat 163 pagina’s!) is het geheel nogal uitgebreid en complex geworden. Het is makkelijk in de doolhof van mogelijkheden de weg kwijt te raken. Verder lijkt meten van de stortgoedeigenschappen bijna altijd onafwendbaar. Zelfs voor de 24 producten die in de norm zijn gegeven, moet de type stroming bekend zijn zodat stromingsproblemen kunnen worden uitgesloten. Met de gegevens in de norm valt hier weinig over te zeggen. Alleen op basis van ervaring met het product of via andere metingen kan meer zekerheid worden gekregen. Ook de voorgestelde methode om spanningsverhouding K rechtstreeks te meten, lijkt niet erg gelukkig. Deze apparatuur is voor zover wij weten namelijk nergens voorhanden.

Belastingen op inserts in silo’s

Inbouwelementen in silo’s en storthopen worden zwaar belast

Inserts

Elementen die ingebouwd worden in silo's worden inserts genoemd. Inserts worden toegepast om de stroming van het bulkgoed in de silo gunstig te beïnvloeden of om de druk in te silo of de belasting op de uitdraagapparatuur te verlagen. Een andere toepassing van inserts zijn de horizontale trekstangen ter ondersteuning van lange silowanden. Ook verticale stangen of kabels om meet- of registratieapparatuur in de silo te hangen zijn omringd door stortgoed en kunnen inserts genoemd worden.
Zie functies van inserts
Al deze inserts hebben invloed op de stroming in een silo maar ondervinden ook belastingen vanuit het opgeslagen materiaal. Helaas bestaat er voor veel situaties tot op heden geen betrouwbare methode om deze belastingen te berekenen, terwijl door het onderschatten van deze lasten nog al eens aanzienlijke schades zijn opgetreden.
Hieronder wordt hier nader op ingegaan.

Belasting op verticale stangen en kabels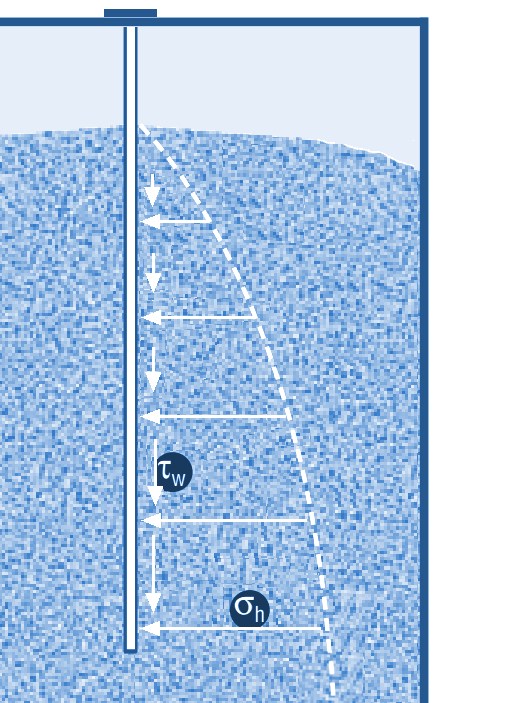

Zolang de kabel of de stang redelijk glad is, dus geen echte ribbels heeft, ontstaat een vrij simpele situatie. Op deze stang werkt vanuit het stortgoed de horizontale normaalspanning. Deze zou de stang willen indeuken, maar daarvoor is geen gevaar. In de verticale richting werkt de schuifspanning. Deze is gelijk aan de horizontale normaalspanning vermenigvuldigd met de wrijving tussen stortgoed en stang/kabel en stortgoed. Omdat de normaalspanning met de diepte toeneemt, zal de schuifspanning over de lengte van de stang/kabel in het stortgoed moeten worden geïntegreerd, om de totale verticale kracht op de stang te berekenen. Omdat de spanning met de diepte toeneemt, zal twee maal zo lange stang een veel meer dan tweemaal zo grote verticale last op moeten nemen.
De normaalspanning kan berekend worden volgens de Euronorm 1991-4. De wandwrijving zal moeten worden gemeten. Voor een stang is dat geen probleem. Bij een kabel moet op een vergelijkbaar oppervlak gemeten worden, of kan de maximale wandwrijving worden afgeschat op basis van de gemeten inwendige wrijving van het stortgoed. Wanneer de stang of kabel echt ruw is aanwezig zijn, zal zich een dunne stilstaande grenslaag kunnen vormen, zodat met de inwendige wrijving gerekend moet worden. De diameter van de stang wordt nu vergroot met tweemaal de gemiddelde deeltjesdiameter. Wanneer er grotere ribbels aanwezig zijn, moet de diameter daarvan, plus een eventuele grenslaag worden aangehouden.

Belasting op horizontale elementen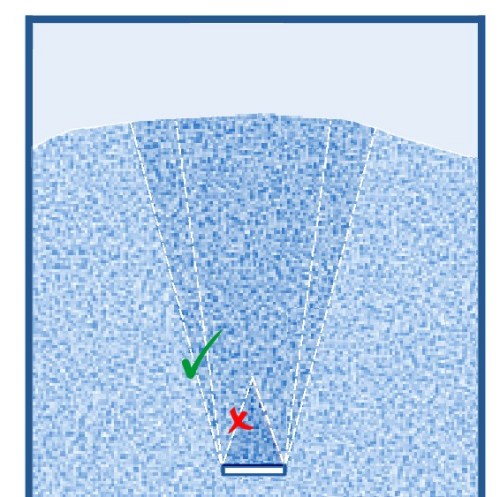

Wanneer in de silo inbouwelementen zijn aangebracht met een zeker oppervlak in horizontale richting, ligt de situatie een stuk ingewikkelder. Het element wordt nu niet alleen verticaal door wrijving belast maar ondervindt ook een verticale belasting door het bovenliggende stortgoed. Deze verticale belasting is aanzienlijk groter dan men misschien zou verwachten. Men stelt zich vaak voor dat er een hoopje product op het element blijft liggen, zodat een dakvorm ontstaat waar het stortgoed langs stroomt zonder het “dak” teveel te belasten.
De praktijk is echter anders: het blijkt dat een inbouwelement een veelvoud van het aangestroomde oppervlak aan belasting opneemt. Hoe kleiner de verhouding van het oppervlak van inbouwelement ten opzichte van dat van de silo, des te groter de factor waarmee de verticale druk op het niveau van de insert moet worden vermenigvuldigd. De geometrie (kegel, plat vlak, trechter) is van mindere invloed. Een lange smalle insert (trekstang) is gunstiger dan een meer vierkant of rond element, maar kan nog steeds erg zwaar belast worden.

Belasting op horizontale trekstangen

De verticale belasting op een trekstang is afhankelijk van de diepte in de silo, de breedte en de vorm van de stang. Omdat de stang een veel grotere verstoring in het materiaal geeft dan alleen het horizontale steunoppervlak (zie figuur hierboven) moet de silodruk ter plaatse worden vermenigvuldigd met een factor. De achtergrond van deze factor is deze: al in de vulsituatie zal het stortgoed in de silo wat inzakken naarmate de vulling toeneemt. Ter plaatse van de stang is echter geen inzakking mogelijk terwijl het materiaal rond de stang wel wat inzakt. Hierdoor ontstaat extra wrijving op het materiaal dat op de stang rust waardoor de verticale belasting dus toeneemt. In hoeverre dit al in forse mate optreedt bij de vulsituatie, hangt af van de zettingseigenschappen van het stortgoed (settling, inklinking) en de silodruk ter plaatse. Bij het leegstromen zal altijd beweging langs en om de stang plaatsvinden met extra wrijving en dus toename van de belasting.

De grootte van de belasting op een aangestroomd oppervlak in een stortgoed is door meerdere onderzoekers experimenteel onderzocht maar heeft tot nogal verschillende resultaten geleid en helaas niet tot een eenduidig rekenmethode. Wel is duidelijk geworden dat de waarde van de belasting op de stang relatief groter wordt bij een kleinere breedte. De vorm van de stang speelt hierbij een rol: bij ronde en ruitvormige stangen is de belasting iets lager dan bij stangen met een vlakke bovenkant. Voor berekening van de belasting op een trekstang in het stortgoed is het zeer uitgebreide onderzoek dat door Kroll is uitgevoerd aan de universiteit van Braunschweig in de zeventiger jaren nog steeds de beste basis. In dit onderzoek is een belastingsfactor bepaald als functie van de breedte van de trekstang, zie de figuur hieronder.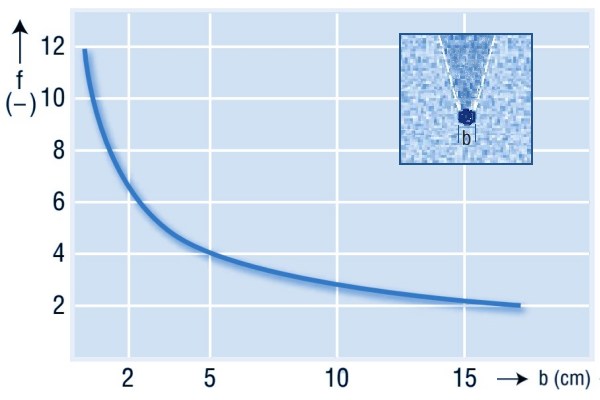
De verticale belasting op de stang wordt berekend door de silodruk (te berekenen volgens de Euronorm 1991.4) op die hoogte te vermenigvuldigen met deze factor en het aangestroomde oppervlak.
Bij smalle en hoge trekstangen (stukken tussenwand) zal ook de verticale wrijving vanuit het materiaal een rol spelen en in de berekening moeten worden meegenomen via horizontale druk en wrijvingscoëfficiënt.

Belastingen op andere aangebrachte elementen

Bij belasting op andere in de silo aangebrachte elementen kan worden gedacht aan inbouwelementen die de stroming moeten beïnvloeden zoals via de wand ondersteunde kegels of trechters of aan kabels hangende meetapparatuur. De belasting is hier in principe op dezelfde wijze te berekenen als hierboven voor trekstangen aangegeven. Ook hier is de belasting op de inbouw veel groter dan het oppervlak en verticale silodruk zouden vermoeden. En ook nu geldt dat een kleine insert een relatief grotere belasting zullen ondervinden. In smalle silo’s geldt dit nog meer, aangezien grotere inserts al snel de maximale druk; de gehele doorsnede maal de silodruk, zullen opnemen.
Naast het aangestroomde oppervlak speelt ook de vorm een rol: een spitse vorm is gunstiger. Net als bij trekstangen is ook voor dit soort inserts geen eenduidige berekening van de belasting bekend. Voor een afschatting van de belasting zou weer gebruik kunnen worden gemaakt van de figuur hierboven. Echter in experimenten met inserts met een lengte ongeveer gelijk aan de breedte, waarvan het oppervlak één-vijftigste deel is van het silo-oppervlak, is gemeten deze wel 20 keer de daar heersende verticale silodruk ondervinden. De vergrotingsfactor is dan dus 20, duidelijk hoger dan op de trekstangen.

Belasting bij omhoog trekken van inserts

Een speciaal geval doet zich voor wanneer getracht wordt een insert met een horizontaal of afgeschuind oppervlak weer uit het materiaal omhoog te trekken. De hiervoor benodigde kracht blijkt in vele gevallen nog zeer veel hoger te zijn dan de (verhoogde) belasting zoals hierboven aangegeven. Een simpel experiment kan dit duidelijk maken. In de figuur hieronder is een cilinder getekend met daarin aan horizontale schijf die aan een kabel of touw hangt. De diameter van de cilinder is iets groter dan de schijf zodat deze laatste zonder wrijving door de cilinder kan bewegen. Wanneer stortgoed in de cilinder wordt gebracht, zal de schijf niet het gehele gewicht van het stortgoed dragen, omdat de cilinderwand via wrijving een deel opvangt. De kracht op de schijf kan met de standaard siloformule van Janssen worden berekend. Wanneer de schijf omhoog wordt getrokken, zal de belasting op de schijf stijgen omdat nu zowel de hele massa stortgoed moet worden opgetild maar ook tegen de wandwrijving in moet worden bewogen. De verticale belasting van de schijf op het stortgoed wordt nu dus hoger. Maar daarmee neemt ook de horizontale belasting toe, omdat deze via de spanningsverhouding (factor K in EN 1991.4) afhangt van de verticale druk. Daardoor neemt, via de wandwrijving, ook de verticale kracht weer toe. De kracht blijkt exponentieel met de materiaalhoogte toe te nemen. Met een kleine materiaalhoogte op de schijf is deze nog omhoog te bewegen, maar bij een vulhoogte van ca. 3 maal de cilinderdiameter is dit onmogelijk.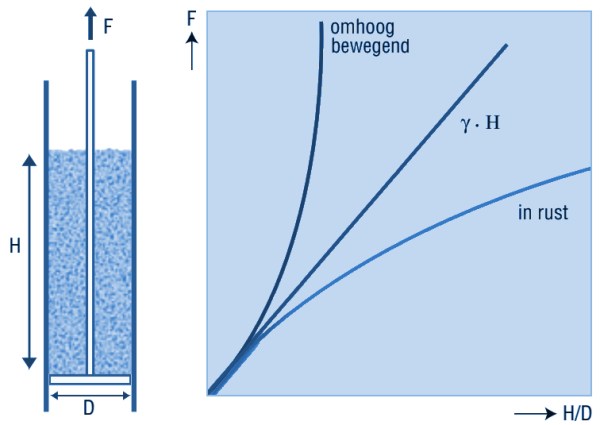
Een dergelijk fenomeen zal ook optreden bij het omhoogtrekken van inserts. Hoewel in de stortgoedmassa door elasticiteit wat meer bewegingsruimte zit dan in een stijve cilinder, zullen ook hier zeer hoge inwendige wrijvingskrachten optreden die het onmogelijk maken de insert op te hijsen wanneer deze nog te diep in het materiaal zit.

Horizontale belasting op verticale inserts

In een silo aanwezige verticale inserts, bijvoorbeeld in de vorm van ontlastingspijpen of mengschroeven, worden in eerste instantie in verticale zin belast door schuifkrachten als gevolg van horizontale druk en wrijving. Deze verticale krachten zijn goed te berekenen met de standaard normberekeningen zodat de constructie hier goed tegen bestand is. In de praktijk zijn het asymmetrische horizontale krachten die de problemen veroorzaken. De horizontale druk in een silo is nou eenmaal nooit geheel gelijkmatig verdeeld – zoals dat bij een vloeistof wel het geval is. Wanneer bij een verticale kolom of pijp aan één zijde meer stroming optreedt, zal de druk daar ter plaatse veel lager kunnen worden. Het gevolg daarvvan is een eenzijdig veel hogere druk, en de bijbehorende buigspanningen. Dit heeft in het verleden meerdere malen tot grote beschadiging van inwendige pijpen geleid. Om deze problemen te voorkomen, is het verstandig bij het dimensioneren er van uit te gaan dat er eenzijdig een volle stortgoeddruk op de pijp staat. Tevens moet rekening gehouden worden met een vergrotingsfactor zoals bij de trekstangen, zie afb. 3.
Het probleem bij stortgoed (in tegenstelling tot bij een vloeistof) is dat er bij een bepaalde vulling wel druk kan zijn, maar dat er geen zekerheid is dat die er is. Daarom mag niet over het algemeen niet gerekend worden op een, voor de constructie positief werkende, steundruk. Alleen in situaties met een voorspelbare en betrouwbare vulling en uitstroom, mag een klein deel van de maximaal werkende druk als steundruk worden gerekend.

Belastingen op tussenconussen

Soms worden tussenconussen in de cilinder aangebracht om de maximale druk in de silo te beperken. Bijvoorbeeld om de kans op trillingen en schokken te verkleinen, of de grootte daarvan te beperken. Een andere aanleiding kan zijn de druk op een uittrekmechanisme voldoende laag te houden. Een dergelijke tussenconus zal een aanzienlijk deel van de verticale silolast ter plaatse overbrengen op de cilinder. De verbinding tussen conus en cilinder zal dus voldoende sterk moeten worden uitgevoerd. Bij de tussenconus zelf kan men uitgaan van de belastingen zoals in de codes beschreven voor een normale conus onderaan de cilinder. Ook de cilinder zelf wordt door het aanbrengen van een tussenconus heel anders belast dan zonder tussenconus, omdat nu lokaal een grote verticale belasting moet worden overgebracht. Tevens zal er een piek in de wanddruk (zie onder) optreden. Vooral bij dunwandige, knikgevoelige uitvoeringen moet hierop worden gelet.

Belastingen op tussenwanden

Het aanbrengen van tussenwanden kan ook als doel hebben om de druk te verlagen, dan wel om ontmenging te voorkomen. De tussenwanden kunnen deze als normale silowanden met de geldende norm worden berekend. De drukken hierop zullen lager zijn dan die op de wanden bij een ongedeelde silo, omdat de celafmetingen nu kleiner zijn. Er moet atlijd vanuit worden gegaan dat een tussenwand horizontaal eenzijdig wordt belast. De schuifspanning op de tussenwand dient wel tweezijdig te worden meegenomen. Een mogelijk steunende werking vanaf de andere zijde mag niet worden meegerekend.

Invloed van inserts op de wanddruk in silo’s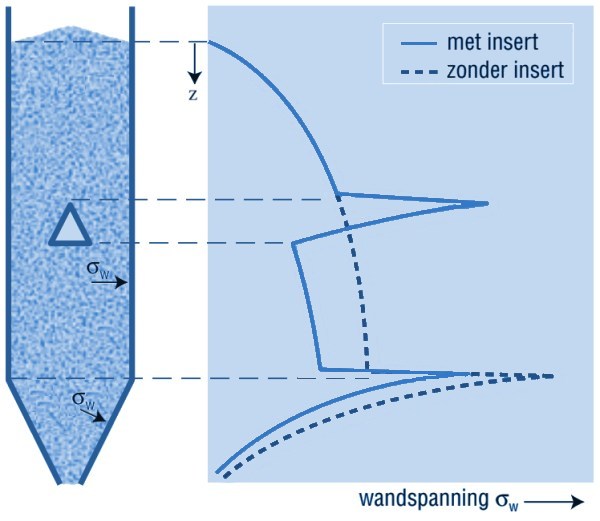

De belasting op inserts moet in de siloconstructie worden opgevangen. Dit zal meestal op de silowand ter plaatse gebeuren. Maar ook wanneer de insert niet op de wand afsteunt, maar bijvoorbeeld geheel door de silobodem wordt gedragen, zal in de meeste gevallen door verstoring van de stroming de wand toch zwaarder worden belast. Het gaat hierbij om de wanddruk: de druk loodrecht op de wand. In de cilinder is dit dus de horizontale druk.
De Euronorm geeft aan dat de invloeden op de silodrukken ten gevolge van het inbouwen van ontlastingskegels, ontlastingsbalken etc. niet door de norm worden gedekt.
Voor de situatie dat inserts worden ingebouwd om massastroming te verkrijgen in een silo die berekend is voor kernstroming, is het tamelijk eenvoudig: er moet nu ook rekening gehouden worden met de plaatselijk hogere (piek)drukken door massastroming. In een silo zonder inserts zal tijdens massastroming een piekspanning aanwezig zijn op de overgang van cilinder en trechter. Wanneer inserts op andere hoogtes in de silo worden gebouwd, moet ook daar met spanningspieken rekening worden gehouden.

Globale inschatting

Helaas is in lang niet alle gevallen een eenduidige berekeningsmethode voorhanden om ongelijkmatige belastingen door verstoring van de stroming te berekenen. Op basis van uit experimenten afgeleide voorstellen is vaak niet meer dan een globale inschatting mogelijk. Misschien dat computersimulaties waarmee de stromingen en spanningen rond inserts kunnen worden bekeken, hier in de toekomst een beter, en voor de praktijk ook bruikbaar antwoord kunnen geven.